Log 7

Justin Vandenbroucke

justinv@hep.stanford.edu

Stanford University

1/3/03 – 1/10/03

This file contains log entries summarizing the results of various small subprojects of the AUTEC study. Each entry begins with a date, a title, and the names of any relevant programs (Labview .vi files or Matlab .m files – if an extension is not given, they are assumed to be .m files).

1/3/03

Strange contours

acousticRect (Linux executable) – rects 36:41

calcFilterValuesMean.m

mergeRectList.m

plotDetectionVolumeRect.m

To review: the scalloped pattern (reproduced in the first plot below from a 12/12/02 entry) was confusing. Simulations were run with greater temporal (dt = 0.7 us) and spatial (dx = 150 m; dy = 0.5 m) resolution. With dt 8 times lower than that used by our experimental ADC, we could sample at 5.6 us 8 different ways. For each point, we did it each of the 8 ways and averaged them together, yielding the second plot below. We see that, in addition to being smoother, the strange vertical bars are removed. However the large-scale scalloping remains.

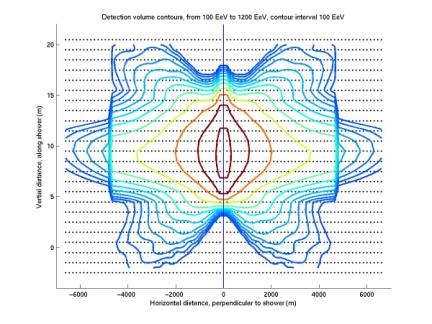
Figure 1

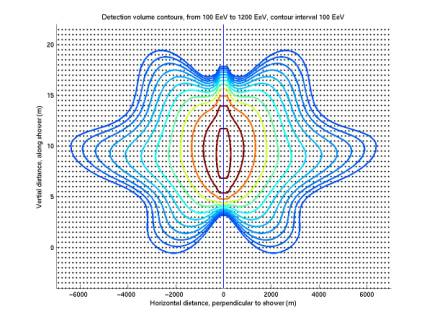
Figure 2

1/3/03

Pressure contours

We have been plotting filter value contours; ie detection contours. Below we plot peak pressure contours to see if the same shape is reproduces. The same general scalloping is present, perhaps to a lesser degree.

The first plot below gives values obtained by generating 8 different time series from the 8 ways of sampling at 5.6 us, and averaging the 8 together. The second plot gives the maximum of the 8 peak pressures. The two are nearly indistinguishable. The third and fourth plots below gives close-ups of the same two plots, in which small differences are apparent.

In summary we see that the scalloping is present in the peak-pressure contours and is not caused by poor time sampling.

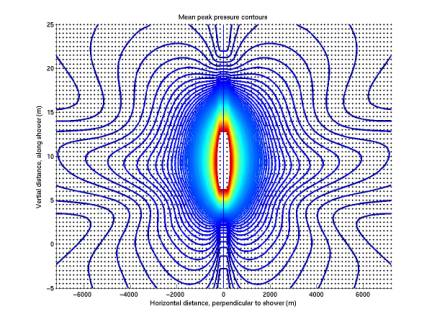
Figure 3

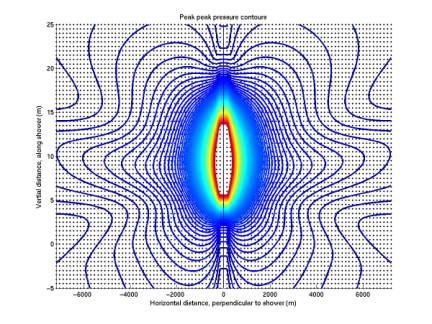
Figure 4

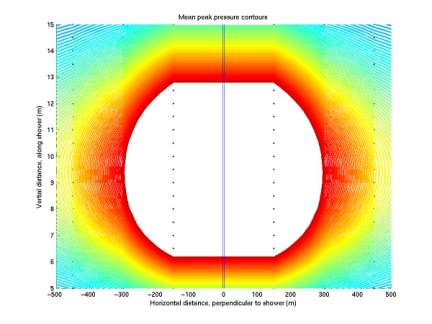
Figure 5

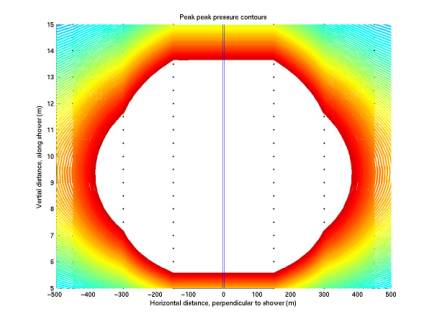Figure 6

10/7/02

Extended cross-section estimates

sigmaEstimate.m

plotSigmaEstimate.m

The plot below gives sigma estimates in the range 10²⁰ eV to 10²¹ eV. Estimates are calculated with a power law given in Gandhi et al, hep-ph/9512364. This is my current target range for our flux limit.

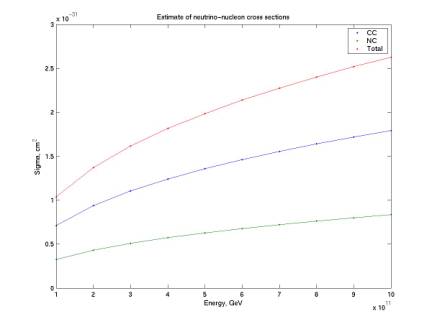
Figure 7

10/8/02

Extended detection contours

acousticRect

calcFilterValuesMean.m

plotDetectoinVolumeRect.m

The first plot below is from rect’s 36 to 41; the second from rect’s 42:47 (each rect is a rectangle of grid points; each has a folder /Data/AUTEC/AUTEC_analysis/acoustic/rectNN/ on erinyes; see …/AUTEC_analysis/text_files/rects.txt for the running parameters given to acousticRect, or look at …/rectNN/input.txt) The first plot is our current best contours for 10²⁰ eV to 10²¹ eV with threshold of 0.05.

Switching to a lower threshold, such as 0.01 (which is attained ~ 5% of running time) – one-fifth as large, yields the same contours as 0.05 with 5 times as large energy (because neutrino energy, peak pressure, and peak filter value are all linearly related). So we need to extend our contours significantly to calculate acceptance with low threshold. This makes sense – we should have very large effective volume and acceptance with a very low threshold. We need a sparser grid to make it larger. The second plot below gives contours with the new grid. They are consistent with the first plot. The second plot shows the contours for higher energies (10²¹ to 10²² eV). They extend to a radius of 20 km! The strange pattern is even stronger now.

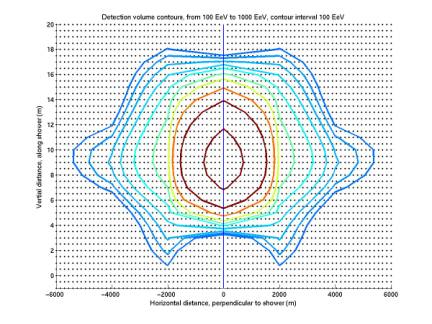
Figure 8

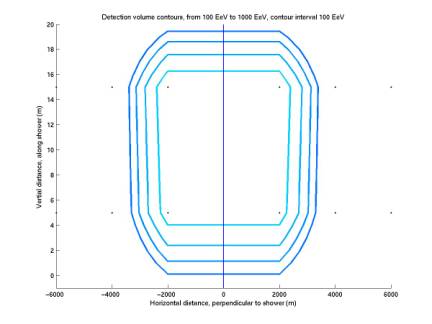
Figure 9

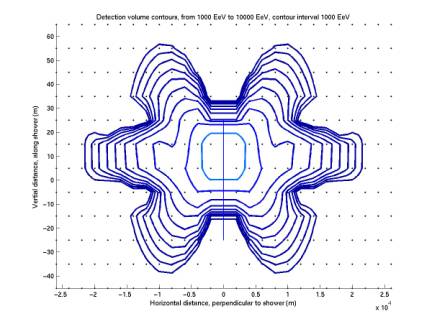
Figure 10

10/8/02

Extended acceptance curves

calcAcceptanceMC.m

calcAcceptanceVsE0.m

plotAcceptanceVsE0.m

plotAcceptanceMultiThresh.m

The first plot below gives acceptance curves extended to the range 10²¹ eV to 10²² eV. All curves are for a threshold of 0.05. Each curve corresponds to requiring a different number of phones hit.

The second plot below gives acceptance curves for various thresholds, all requiring 4 phones hit. They were all generated by using the 4-phone curve from the first plot below and simply rescaling the energies, maintaining the same values for acceptance: E = E₀ * thresh / thresh₀. The 0.05 threshold curve in the second plot is the same as the 4 phone curve in the first plot.

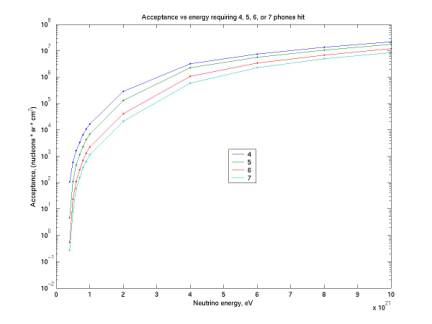
Figure 11

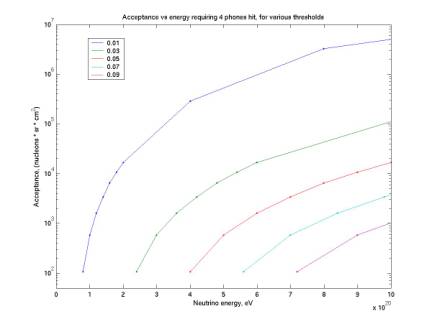
Figure 12

1/11/03

More exploration of fringing pattern

plotDetectionVolumeRect.m

plotNumbers.m

plotWaveforms.m

gridFilter.m

The first plot below reproduces a previous plot, with different coloring and labels indicating particular grid points. The second plot gives the simulated pressure waveforms at each grid point. Note that the contours represent peak filter values, while the time series are for pressure. As shown above, the fringing pattern is present in both peak-pressure and peak-filtered pressure contours. The table below gives peak pressure values and peak filtered-pressure values.

The fringing seems to a kind of diffraction pattern from the line source. We do not expect simple spherical wavefronts because the source is not spherical. Considering that the waveform at a particular grid point is the superposition of all the waves generated along the line, the points along each radius from the center of the contours the correspond to a different

For spherical contours we would expect signals at points 1, 2, 3 to be similar, and those at 4, 5 to be similar. However as shown in the table and the contours, 3 has a lower value of both pressure and filter value than 1 and 2. 3 and 4 actually have similar waveforms, and peak pressures, with 3 stretched in time relative to 2. So apparently 4 has a width that matches the response function better. The fringes are then present in both pressure and filter contours, but stronger in filter contours.

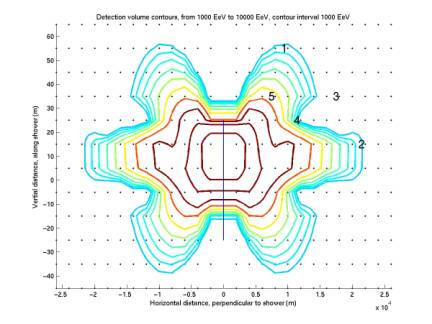
Figure 13

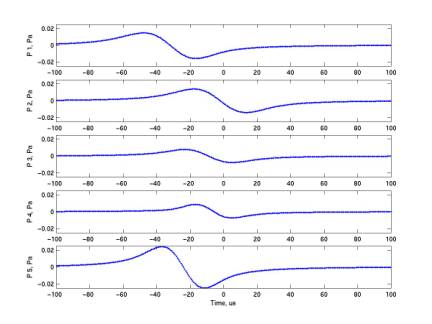
Figure 14

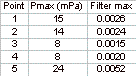
Table 1