Log 13

Justin Vandenbroucke

justinv@hep.stanford.edu

Stanford University

3/11/03

This file contains log entries summarizing the results of various small subprojects of the AUTEC study. Each entry begins with a date, a title, and the names of any relevant programs (Labview .vi files or Matlab .m files – if an extension is not given, they are assumed to be .m files).

Note: Higher-resolution versions of the figures are available. If a log has URL dirname/logLL.html, Figure FF of the log should be at URL dirname/FF.jpg.

3/11/03

Distribution of event energies

plotEstimateEnergies.m

Once a coincidence of 4 single-phone events have been found, a 4-phone event position can be estimated. With this position estimate, the event energy can be estimated. Figure 1 gives the spectrum of these event estimates. Preliminary positons were used. Only events taken during quiet minutes (threshold < 0.025) and with few cycles (ntyp < 4) were included. Note that the mean energy is ~10^21 eV.

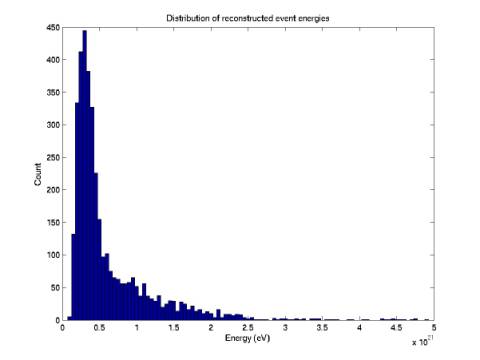
Figure 1

3/14/03

Restriction of effective volume

plotAcceptanceVsE0.m

Most of our acceptance calculations have assumed infinite effective volume in all directions. But it is useful to restrict our effective volume to a cylinder with radius ~10 km. Beyond this distance, ray bending becomes significant, and position reconstruction becomes difficult. It also becomes difficult to assure that the water is not blocked by the sea floor beyond this distance. Figure 2 compares the acceptance with infinite volume with that cut off by the 10 km cylinder (the lower set of 4 curves represents that cut off by the cylinder). All curves are for a threshold of 0.02, the maximum quiet threshold.

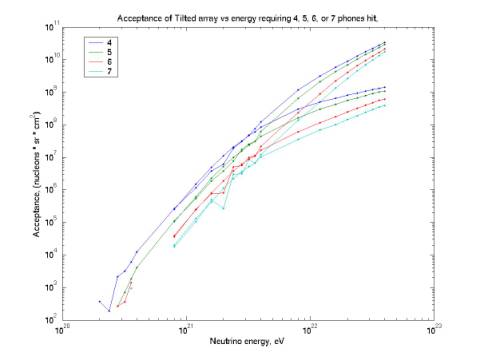
Figure 2

3/16/03

Effective volume considering radiation pattern

plotEffVol.m

We can reject events by considering the extreme shape of the radiation pattern expected from neutrino events. Directly above the detector, there is no orientation for which the radiation pattern will intersect at least 4 phones. Farther away from the detector horizontally, events above the detector can be tilted to an orientation that will intersect at least 4. The farther the horizontal distance, the higher the maximum height above the detector at which events can be detected. We can plot r (radial distance from central phone) vs. z (height above detector plane) of the events (with any orientation) that can trigger 4 phones. Figures 3-6 give such plots.

These plots map the effective volume of the detector (cut off by a cylinder at 10 km). In Figure 3, the radius of the radiation disk is only ~5 km, which means there is a maximum r for the effective volume. In Figure 4, the maximum radius reaches the bounding cylinder at 10 km. In Figure 5, the maximum height at this radius continues to increase. In Figure 6, the maximum height has ceased to grow.

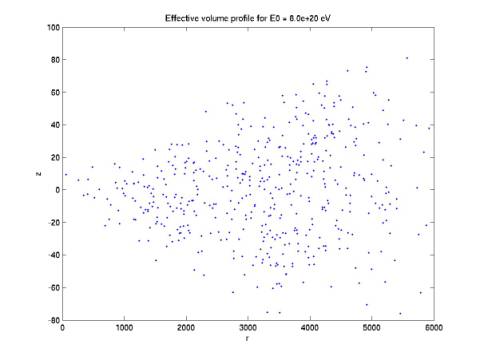
Figure 3

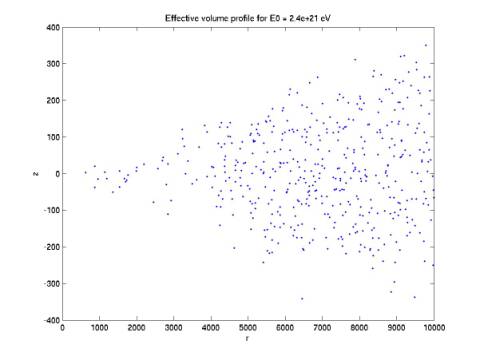
Figure 4

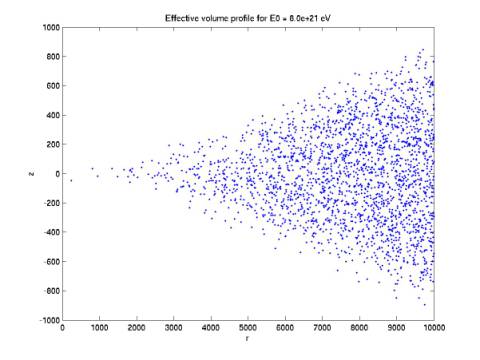
Figure 5

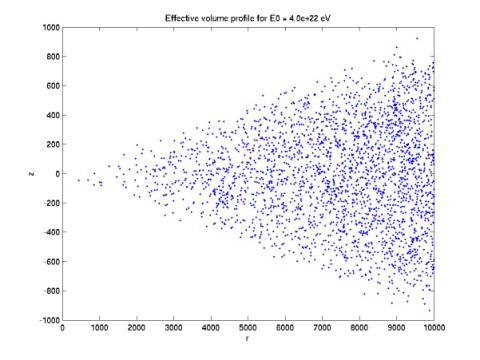
Figure 6

3/16/03

Effective cone bounding curves

plotEffVol.m

We see that for a given neutrino energy, the effective volume is bounded by a cone. Figure 7 gives the curves bounding these cylinders for various energies. The lowest curve terminates at a maximum radius less than the 10 km cut off. Note that at ~10^22 eV the bounding cone stops growing with energy. We can require that reconstructed events lie below these curves if they are neutrinos.

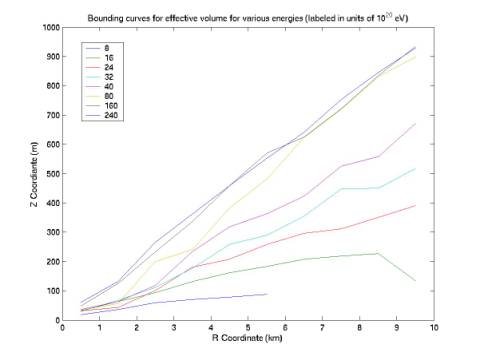
Figure 7