Log 23

Justin Vandenbroucke

justinv@hep.stanford.edu

Stanford University

This file contains log entries summarizing the results of various small subprojects of the AUTEC study. Each entry begins with a date, a title, and the names of any relevant programs (Labview .vi files or Matlab .m files – if an extension is not given, they are assumed to be .m files).

Note: Higher-resolution versions of the figures are available. If a log has URL dirname/logLL.html, Figure FF of the log should be at URL dirname/FF.jpg.

4/5/04

New cut: dt₀ < 1 ms

calcDt0Hist.m

plotDt0Hiist.m

I introduced a new cut that helps with event rate stabilization, particularly coincidence-event rate stabilization. For each event written to disk (whether code 0, 1, or 2 – that is whether it passed online trigger level 2 or not), let dt₀ be the difference between the event’s time stamp and the previous event on disk’s time stamp. The distribution of log10(dt₀/s) is shown in Figure 1. There is a large spike at 0.5 ms. Events are captured as follows: the triggering sample (the first sample above threshold) is set at the center of the 179-sample (1 ms) capture window. Then the search for samples above threshold is re-commenced after the window ends. So when there is a brief very noisy period, there might be a train of 50-100 events separated by exactly 0.5 ms. These lead to very large combinatorics during coincidence windowing.

So a new cut is to remove all events with dt₀ < 1 ms. For event i, dt₀(i) = t₀(i) – t₀(i-1). This effectively cuts out all periods with rapid-fire triggering, and introduces a new (very small) dead time. This removes the large spike below –3 in Figure 1.

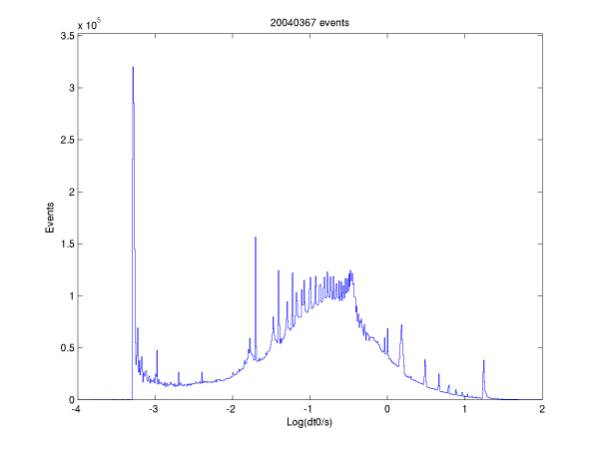
Figure 1

4/5/04

New event map

applyCutSet.m

localize5Coin.m

plotLocalize5Coin.m

After applying the new cut set (cut set 2), there are 948 5-phone events that are localized. These are shown in Figures 2 and 3. The red lines delimit our neutrino fiducial volume. All events are shown, including those that did not converge well enough to be considered a valid localization (this includes the events in the arc outside the red circle in Figure 2 – these lie on the outer edge of the lookup grid of locations used to find a first guess for localiation).

We can further require that the localization metric m < 0.01, and that events are localized within the fiducial volume. This results in 2 surviving events.

For now I am not including the effect of localization precision (~10-100 m). To do this correctly we will probably have to relax the fiducial volume cut a bit (make it fuzzy according to the precision).

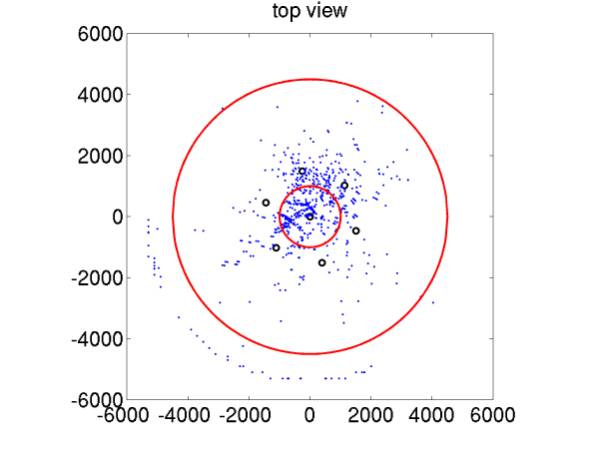
Figure 2

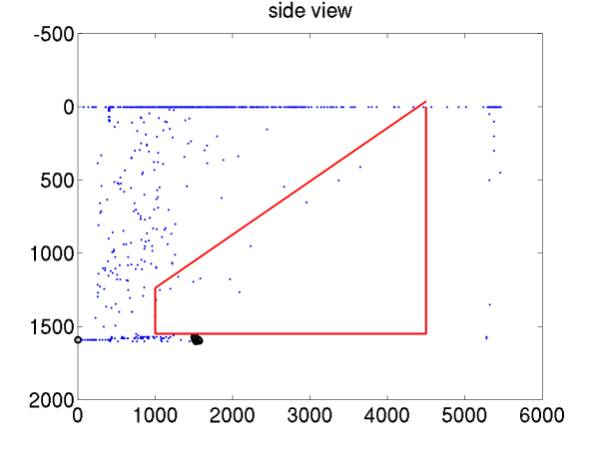
Figure 3

Figure 4

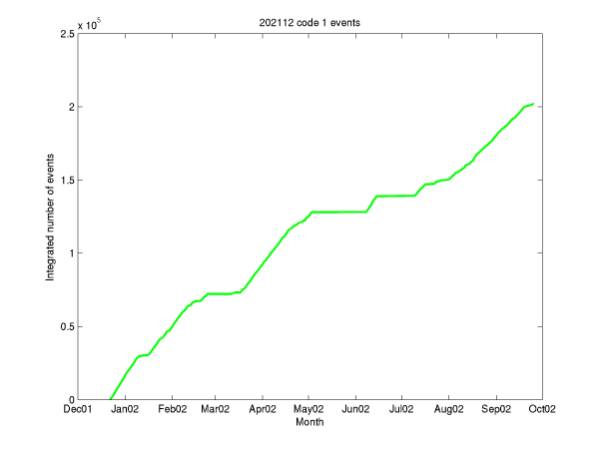
Figure 5

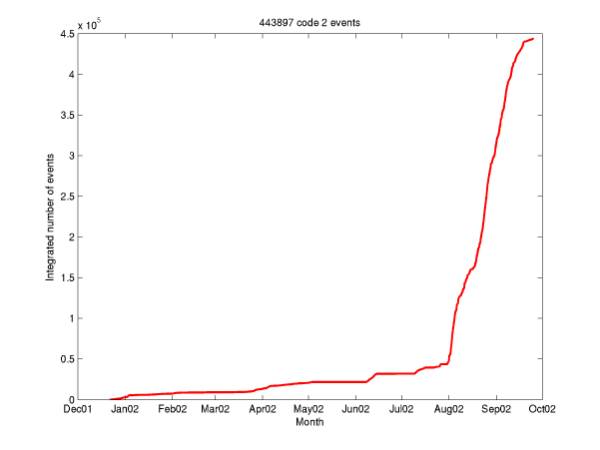
Figure 6

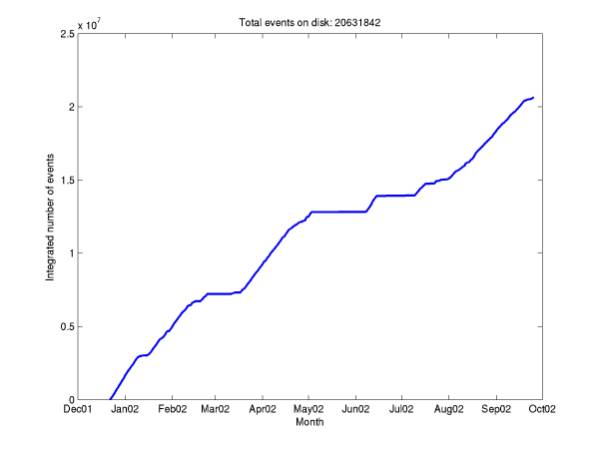
Figure 7

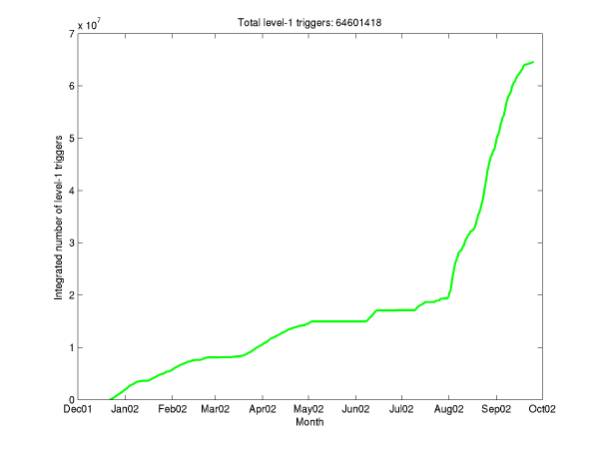
Figure 8

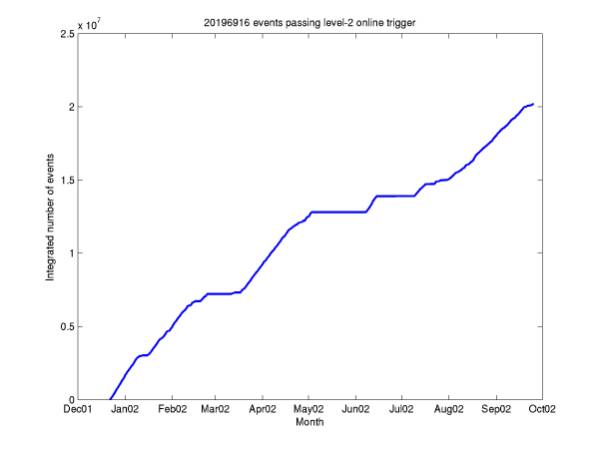
Figure 9

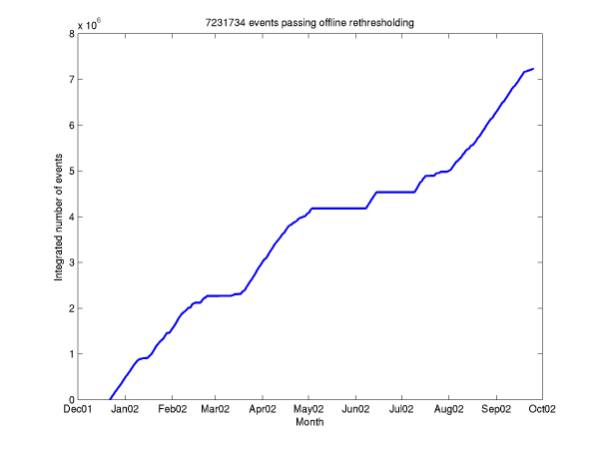
Figure 10

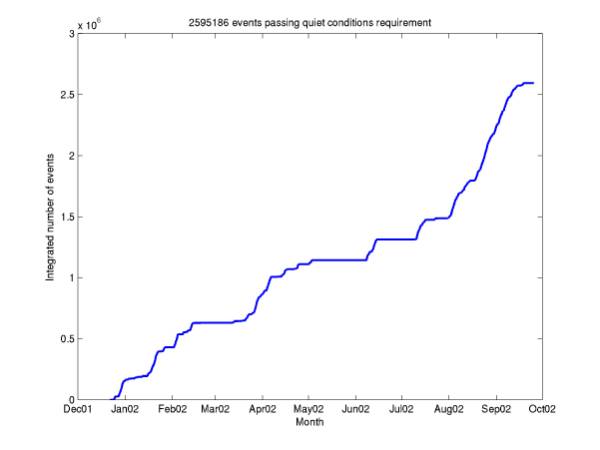
Figure 11

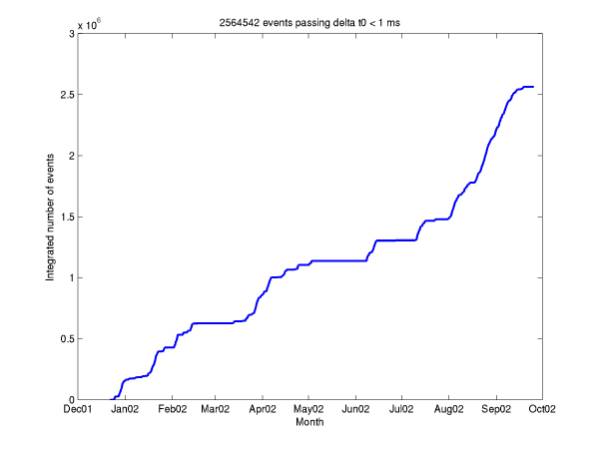
Figure 12

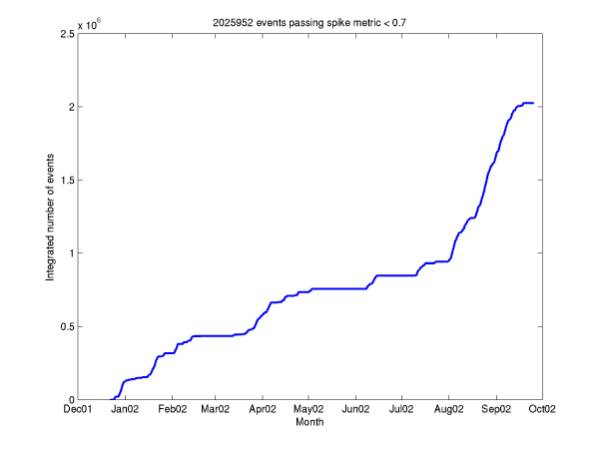
Figure 13

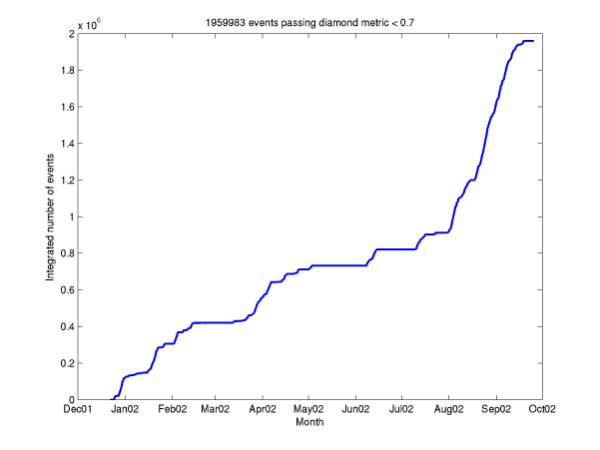
Figure 14

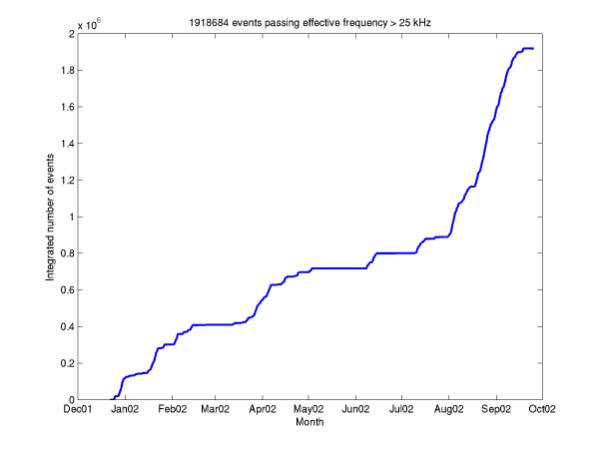
Figure 15

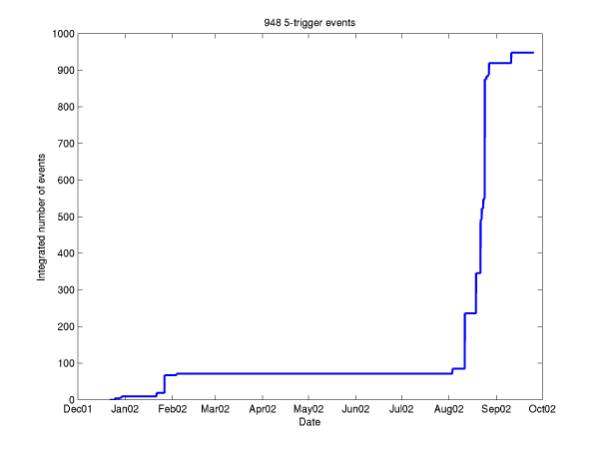
Figure 16

Figure 17

Figure 18